回帰分析とは、ある数値の結果を別の数値のを使って説明する手法のことです。
結果を求める数値のことを目的変数、目的変数を求めるために使われる数値のことを説明変数と呼びます。
少し難しい言い方をすると、回帰分析とはY = f(X)というモデルを当てはめるて分析する事です。fとはfunction(関数)のことで、説明変数(X)を関数に与えることで目的変数(Y)を求めることができます。

例として、目的変数をアイスの売上とします。このアイスの売上を求める際の説明変数として考えられるのは、気温・天気などが考えられます。
単回帰分析
回帰分析は、様々なモデルを使って分析を行います。よく使われるモデルとして線形回帰のY = AX + Bというものがあります。
これは単回帰分析とも呼びます。
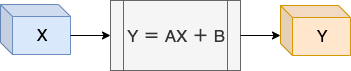
単回帰分析は、目的変数を求めるのに1つの説明変数を使います。
アイスの売上を単回帰分析に当てはめると、アイスの売上は気温との関係がありそうなので単回帰分析ができると言えます。
以下のようなアイスの売上と気温のデータがあったとします。ぱっ見た感じ、売上と気温の関係が分かりにくいです。
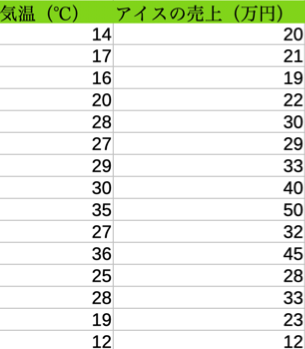
これをグラフにすると気温が上がるとアイスの売上も上がっていることが分かります。
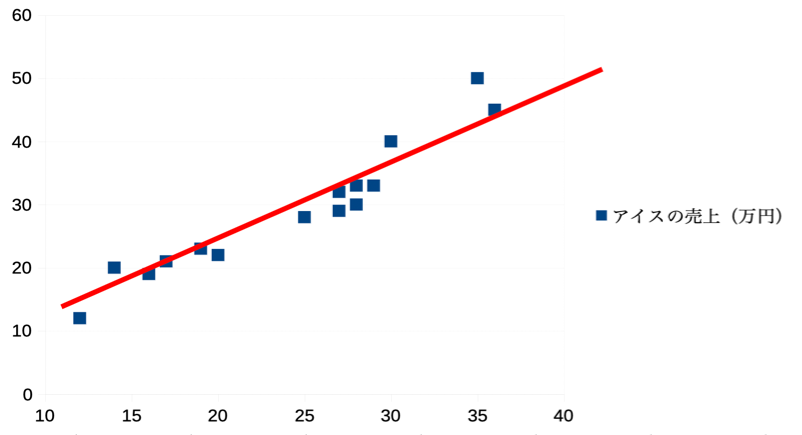
分析の入門として理解しやすい問題ですね。
重回帰分析
単回帰分析というものがある一方で、複数の説明変数を使う重回帰分析というものもあります。
単回帰分析は1つの目的変数を1つの説明変数で求めました。これに対して重回帰分析は、1つの目的変数を複数の説明変数で求めます。
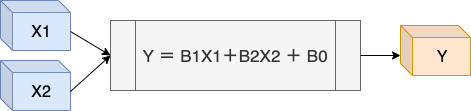
アイスの売上を重回帰分析に当てはめると、気温の他に、お店の場所・従業員数・広告費などが売上に関係していると考えることができます。
ちょっと難易度が上がりましたね。
実際に分析をしようとしたときには、目的変数を求めるために関係のありそうな説明変数を自分で探す必要があります。
関係がありそうなデータを収集していく必要もあるのですが、データを分析できる形に変更する必要があったりします。
データの選定、データの収集は重要な作業と言えます。



